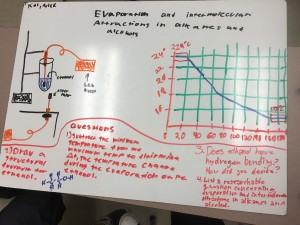
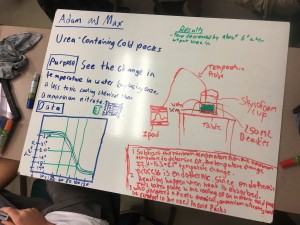
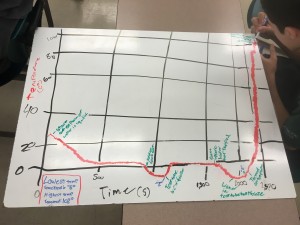
There is a quote from the Ancient Mariner by Coleridge: “Water, water, everywhere, Nor any drop to drink”. One of the continuing investigations for us this year is the issue of water. It ties nicely with some of the physical chemistry work that we are trying to do. Water has so many wonderful properties that make it special, including life on earth itself. The chemistry of water and its role in society provide so many different ways that we might approach it. Today, our work centered around our community water supply, where it comes from, how it is distributed, what are the ways that the Native Hawaiian people viewed this, and probably most pressing: is it safe to drink and is it secure?
We took a field trip today to the Waihee Water Tunnel (info here). We were ably guided by Arthur Aiu, community relations specialist for the board of water supply. After a 1.5 mile hike in, we entered a tunnel that extended into the mountainside for over 1/4 mile (1500 feet) and came upon the water that is directed to most of the communities on the windward side of the island. The graphic below gives you a sense of where the water comes from.
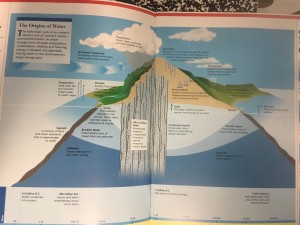
Info graphic that explains how water comes to the islands and is stored through a natural process
The purpose of this post is not really to teach you about where our water comes from, but it’s worth mentioning that Hawaii is really a special place in how the conditions of weather and mountains produce large reserves of water that are located both in compartments in the mountains called Dikes, as well as aquifers below the island that hold water. The students learned about how the water gets there, how it’s removed, why it’s handled the way it is and even what safety concerns there are about water quality and how the board of water supply manages that. For example, Arthur mentioned that all water on Oahu is treated with small amounts of chlorine to control for bacterial growth – that’s something that I had not been aware of, but we know from our chemistry work the reactive nature of chlorine and students should have been making the connection to why chlorine is such an ideal substance to interact with living matter to break apart contaminants. In other parts of the island where the water has become more contaminated from organic pesticides, activated charcoal is used. Another example of chemistry helping keep our water drinkable.
As you can see from the pictures posted below, and more here (Flickr account here) the water literally filters down through the rocks and drips through the fissures that have occurred through different volcanic events that have happened over time. The water that we were observing only takes about nine months to filter from the rainfall down through the mountain to these caverns, although it takes 25 years or more for the water to filter all the way down to the aquifer located below the island. The challenge for the students was to really consider how do we protect and ensure this precious resource since all we can plan to use is the water that we have here on the island.

Hiking into the valley

Arthur AiuExplains the way that the water collects in Hawaii’s mountains and aquifers

Our happy group before entering the tunnel

Arthur Aiu Explains both the Hawaiian legends around the water, as well as the structure of the compartments in the bulkheads

This leads us to the bigger question that were going to explore over the next couple of months. Our visit today was water that feeds the Windward communities, but there is a bigger problem brewing in Honolulu because the main source of water there at Halawa is in danger of serious contamination from fuel tanks that were placed above the source of water by the Navy in the 1940s (short history of that here , excellent presentation slides from Auguust 2016 meeting here ). Our next steps for the class are to understand this problem more deeply, attend the October 6 public hearing that will have presentations by both the Navy, and the board of water and start working with our city Council to figure out ways that our students might be able to be helpful. Our ultimate goal is to present information to the City Council in November to have them better understand the issues that are affecting our community and this problem. As always, our good work continues as our learning gets deeper…

Information about the October 6 meeting about the water situation at Red Hill/Halawa