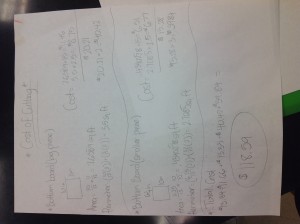One of the challenges in secondary mathematical education is finding the space between computation and thinking. Often times, the mathematical work we do in traditional math classes centers around solving particular kinds of mathematical algorithms. Most of us remember learning how to do a two column proof, learning how to factor a polynomial, or finding the slope of the line. The famous question “when are we ever got a use this stuff?” is not just a trivial query in the part of our students, but a legitimate question about the applicability of the procedural math we learn and is considered an important part of our math scope and sequence. Algebra, geometry, advanced algebra, statistics, precalculus, calculus… The sequence of math has its own inherent hierarchy and one of the challenges is on a day-to-day basis finding meaningful ways to give students opportunities to practice and apply this knowledge in useful ways. We know from research, that the more we can anchor this in real experiences, the mathematics will be tied to more than just a series of rote steps, but to actual principles of science, architecture, economics, population studies, etc.
In our MPX planning, we try and balance this sometimes mutually exclusive way of learning math – math rules, and math function. I have included a couple of examples that seem simple, but turn out to be more challenging than they might seem.
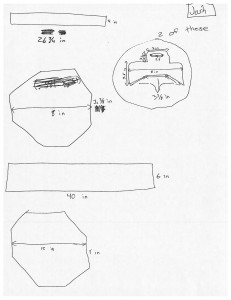
The first two graphics below are examples of students doing a cost analysis for the aquaponics project that they are building in our class. The main structure will be composed of plexiglass, and the measurements for the deconstructed shape need to be accurate, and understood as their individual deconstructed geometric shapes. One local manufacturer gave our students a pricing structure that was based both on the area ($15 per sq ft) of plexiglass needed, as well as the lineal foot measure ($2.50 per lineal ft) – the perimeters for the shapes. The challenge for our students was calculating the actual cost for materials and cutting for the shapes. As a result, they needed to apply their understanding of perimeter and area, as well as take into account ratio thinking about cost per item and doing an aggregate total for their object. As you can see, one group actually had an octagon is a part of their shape, which presented wonderful opportunity to look at area formulas for polygons.
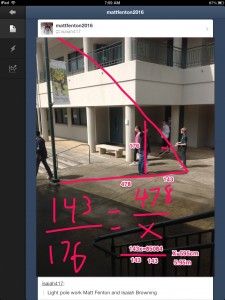
The next two pictures show another problem that came up which is a more traditional application mathematically, but still give students a chance to practice their thinking in a real scenario. Students were asked to calculate the height of a light pole in our Watase courtyard using their understanding of similar triangles, which we had done a more traditional math lesson on earlier in the week. Sometimes in our work, we do start with core concepts in geometry that we know must be covered, even if there isn’t a perfect fit to a project that we have – the ugly deal we need to make with the devil to both do original authentic work, and yet still cover the basic concepts in our geometry and biology series that are part of the ninth-grade experience.
So one of the challenges that we have is looking at any particular domain of knowledge in our geometry series and continually asking is there a way to backward map from one of our projects to this content. This is not always possible. The next possibility for us is to hopefully find something inherently interesting in a particular content sequence that we can map to. My favorite example of this is the one that mathematician Dan Meyer shows in his tent lecture below:
so where do these ideas come from? We often look through many different than textbooks, to see what kind of end of chapter problems (like Dan did) to find something that would be engaging, authentic, and serve the purpose of learning and reinforcing the concept correctly. Sometimes we can find these fairly easily (like the poll activity mentioned above) other times hours of searching for inherently interesting examples turn out fruitless. As we build a repertoire of activities, over the years we will probably have a more refined way to define, create and refine activities that are successful… But the search continues to try and find the match between authentic mathematical thinking, and learning the kind of computational skills that are inherent on standardized testing and expected at higher levels of mathematics coursework they may encounter. An ongoing challenge…